寻找一个数的二分查找(搜索区间两端都闭)

int binarySearch(int[] nums, int target) {
    // 搜索区间是左闭右闭[left, right]
    int left = 0;
    int right = nums.length - 1; // 注意
    
    // 终止条件时，left == right + 1
    while (left <= right) {
        // 计算mid时需要防止溢出
        int  mid = left + (right - left) / 2;
        // 停止的终止条件，找到了target
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1; // 注意
        } else if (target < nums[mid]) {
            right = mid - 1; // 注意
        }
    }
    // 终止时仍未找到target
    return -1;
}

• 为什么while循环的条件中是<=，而不是<？
  • 因为初始化right的赋值是 nums.length - 1，即最后一个元素的索引，而不是 nums.length
  • 这两者会出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间[left, right]，后者相当于左闭右开区间[left, right)，因为索引大小为nums.length是越界的
  • 这个算法使用的是前者[left, right]两端都闭的区间。这个区间其实就是每次进行搜索的区间
  • while(left <= right)的终止条件是left == right + 1，写成区间的形式就是[right+1, right]，或者代个具体的数字进去[3,2]，可见这时区间为空，因为没有数组大于等于3且小于等于2。这时while循环终止是正确的，返回-1即可
  • while(left < right)的终止条件是left == right，写成区间的形式是[left, right]，或者代个具体的数字进去[2,2]，这时区间非空，还有一个数2，但此时while循环终止了。即2被漏掉了，索引2没有被搜索，如果这时直接返回-1就是错的

寻找一个数的二分查找(搜索区间左闭右开)

• 当然，如果非要用while(left < right)也可以，需要打一个补丁

//...
while (left < right) {
    // ...
}
return nums[left] == target ? left : -1;

寻找左侧边界的二分查找(搜索区间左闭右开)

// 寻找到的左侧边界的索引下标i即，nums 中小于 target 的数有 i 个
// 换句话说，如果 target 要插入到 nums 应插入到位置 i
// 如对有序数组nums=[2,3,3,5,7]
// target=1，算法会返回0，含义是：nums中小于1的元素有0个
// target=3，算法会返回1，含义是：nums中小于3的元素有1个
// target=8，算法会返回5，含义是：nums中小于8的元素有5个
int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    // 搜索区间为左闭右开[left, right)
    int left = 0;
    int right = nums.length; // 注意
    
    // 终止条件时，left == right
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 找到target时不要立即返回，而是收缩右侧边界
            // 在区间[left, mid)中继续搜索
            // 若此时 mid 已经达到了左侧边界，那后续只会变动 left,
            // 直到 left == right终止
            right = mid;
        } else if (nums[mid] < target) {
            // 搜索区间变为[mid+1, right)，此时 mid 和左侧数已被排除
            left = mid + 1;
        } else if (target < nums[mid]) {
            // 搜索区间变为[left, mid)，此时 mid 和右侧数已被排除
            // 但 right == mid，可保证若 target 不存在 nums 中时，
            // 最终返回下标在 target 该插入的地方
            right = mid; // 注意
        }
    }
    // 达到终止条件时，此时若需返回target需插入的索引下标直接返回
    // left 可返回的取值范围是[0, nums.length]闭区间

    // 若需使 target 不存在 nums 中返回 -1, 则需分两种情况判断
    // 1. target 比所有数都大，数组已越界，需用长度来判断，
    //    其实left最大也就==长度，不会>，此处是防御性编程
    // 2. target 不存在 nums 中
    if (left >= nums.length || nums[left] != target) 
        return -1;
    
    return left;
}

• 为什么while 中是<而不是<=
  • 因为right = nums.length而不是nums.length-1。因此每次循环的「搜索区间」是[left, right)左闭右开
  • while (left < right)终止的条件是left == right，此时搜索区间[left, left)为空，所以可以正确终止
  • 对于搜索左右侧边界的二分查找，这种写法比较普遍

寻找左侧边界的二分查找(搜索区间两端都闭)

• 可以，只要明白「搜索区间」的概念，就能有效避免漏掉元素
• 因为要求搜索区间两端都闭，所以right应该初始化为nums.length - 1，while的终止条件应该是left == right + 1，即用<=

int left_bound(int[] nums, int target) {
    // 搜索区间为[left, right]
    int left = 0, right = nums.length - 1;
  
    // 终止条件时，left == right + 1
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 收缩右侧边界，若此时已达到左侧边界，那此时 right 指向
            // 左侧边界-1的索引，以后只会收缩左侧边界，直到left == right+1
            right = mid - 1;
        } else if (nums[mid] < target) {
            // 搜索区间变为[mid + 1, right]
            left = mid + 1;
        } else if (target < nums[mid]) {
            // 搜索区间变为[left, mid-1]
            right = mid - 1
        }
    }
    // 达到终止条件时，此时若需返回target需插入的索引下标直接返回
    // left 可返回的取值范围是[0, nums.length]闭区间
    
    // 检查越界情况和是否存在
    if (left >= nums.length || nums[left] != target)
        return -1;
    // 返回 left 和 right+1均可
    return left;
}

• 之所以要检查越界情况，是因为由于while的退出条件是left == right + 1，所以当target比nums中所有元素都大时，会存在以下情况使得索引越界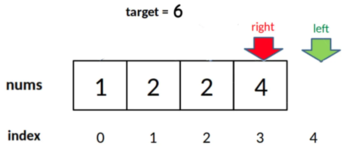
• 

寻找右侧边界的二分查找(搜索区间左闭右开)

• 只有两处和搜索左侧边界不同

int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;
    
    // 终止条件时，left == right
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 找到target时不要立即返回，而是收缩左侧边界
            // 在区间[mid+1, right)中继续搜索
            // 若此时 mid 已经达到了右侧边界，那后续只会变动 right,
            // 直到 left == right终止，此时 left 指向右侧边界+1的下标
            //
            // 即 while 循环结束时，nums[left] 一定不等于 target 了
            // 而 nums[left-1] 可能是 target
            left = mid + 1; // 不同点1
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (target < nums[mid]) {
            right = mid;
        }
    }
    // 达到终止条件时，left==right 指向的是右侧边界+1的下标
    // left 可返回的取值范围是[0, nums.length]闭区间
  
    // 若需使 target 不存在 nums 中返回 -1, 则需分两种情况判断
    // 1. target 比所有数都小，此时 left == 0，< 号为防御性编程
    // 2. target 指向的右侧边界不存在 nums 中
    if (left <= 0 || nums[left-1] != target)
        return -1;
    
    // 返回右侧边界
    return left - 1; // 不同点2
}

寻找右侧边界的二分查找(搜索区间两端都闭)

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // 终止条件时，left == right + 1
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            // 收缩左侧边界
            left = mid + 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    // 此时，left - 1 == right
    // left 的含义仍是指向的是右侧边界+1的下标，可返回 left-1 或 right
    // left 可返回的取值范围是[0, nums.length]闭区间
    // right 是指向右侧边界，取值范围是[-1, nums.length-1]闭区间
    
    // 若需使 target 不存在 nums 中返回 -1, 则需分两种情况判断
    // 1. target 比所有数都小，此时 left == 0，< 号为防御性编程
    // 2. target 指向的右侧边界不存在 nums 中
    if (left <= 0 || nums[left-1] != target)
        return -1;
  
    return left - 1; // 或直接返回 right
}

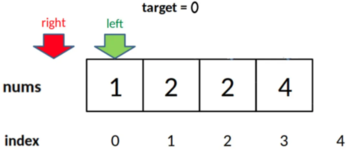
• 当target比所有元素都小时，right会被减到-1，所以需要在最后防止越界
• 

记忆六种二分查找的函数方法

• 1.确定使用的是两端都闭还是左闭右开的写法
  • 采用两端都闭的写法时(除在查找左侧和右侧边界外4种，查找一个数的左闭右开当作两端都闭)
    • 初始化为left = 0; right = nums.length - 1
    • 循环判断规则为left <= right
    • 结束时left == right+1
    • 判断规则如下

  else if (nums[mid] < target) {
      left = mid + 1;
  } else if (target < nums[mid]) {
      right = mid - 1;
  

  • 采用左闭右开的写法时(仅在查找左侧和右侧边界)
    • 初始化为left = 0; right = nums.length
    • 循环判断规则为left < right
    • 结束时left == right
    • 判断规则如下

  else if (nums[mid] < target) {
      left = mid + 1;
  } else if (target < nums[mid]) {
      right = mid;
  

• 2.确定哪种二分查找以及查找过程中mid的意义
  • 查找一个数(两端都闭)+查找一个数(左闭右开)：判断当前mid是否为要找的数：是的话直接返回return mid;
  • 寻找左侧边界(左闭右开)：此时均应该收缩右边界，因右为开区间，即把 right 当作新边界，right = mid;
  • 寻找左侧边界(两端都闭)：此时均应该收缩右边界，因右为闭区间，需把 right-1 当作新边界，right = mid - 1;
  • 寻找右侧边界(左闭右开+两端都闭)：此时均应该收缩左边界，左边均为闭区间，即left = mid + 1;
• 3.确定哪种二分查找结束时left、right变量对应的意义和取值范围，以及不存在时需补判断的内容
  • 查找一个数(两端都闭)：此时区间已被搜索完，直接返回-1即可
  • 查找一个数(左闭右开)：此时相比两端都闭，少判断了left元素，所以需补上：return nums[left] == target ? left : -1;
  • 寻找左侧边界(左闭右开)：此时 left == right 为返回 target 需插入的索引下标，所以需返回left，left 取值范围是[0, nums.length]闭区间，所以需补判断left >= nums.length || nums[left] != target成立返回-1
  • 寻找左侧边界(两端都闭)：除了结束时 left == right + 1 外，left 的意义、取值范围、补判断内容均同左闭右开
  • 寻找右侧边界(左闭右开)：此时 left == right 指向的是右侧边界+1的下标，所以需返回left-1，left取值范围是[0, nums.length]闭区间，需补判断left <= 0 || nums[left-1] != target成立返回-1
  • 寻找右侧边界(两端都闭)：此时 left == right + 1，left 的意义、取值范围、补判断内容均同左闭右开，但此处可返回left-1或right，或以 right 判断right < 0 || nums[right] != target也可

现有语言的二分查找库函数调用

• C++

#include <iostream>
#include <algorithm>
#include <vector>
int main()
{
    // 二分查找
    std::vector<int> nums = { 1, 2, 4, 5, 5, 6 };
    if (std::binary_search(nums.begin(), nums.end(), 待查找数)) {
        std::cout << "Found " << '\n';
    } else {
        std::cout << "not Found!\n";
    }
  
    // 找第一个大于待找元素的元素，事实等于找右侧边界+1
    auto upper = std::upper_bound(nums.begin(), nums.end(), 待查找数);
    if (upper != data.end()) {
        std::cout << "Found " << upper << " at index " 
          << std::distance(data.begin(), upper) << '\n';
    } else {
        // 待查找数超过范围
        std::cout << "not Found!\n";
    }

    // 找第一个小于等于待找元素的元素，事实等于找左侧边界
    auto lower = std::upper_bound(nums.begin(), nums.end(), 待查找数);
    if (lower != data.end()) {
        std::cout << "Found " << lower << " at index " 
          << std::distance(data.begin(), lower) << '\n';
    } else {
        // 待查找数超过范围
        std::cout << "not Found!\n";
    }
}

• Python3
  • 参考：https://docs.python.org/zh-cn/3.6/library/bisect.html
  • 查找左侧边界并返回index：bisect.bisect_left(a, x, lo=0, hi=len(a))
  • 查找右侧边界+1并返回index：bisect.bisect(a, x, lo=0, hi=len(a))
  • 其中 a 是 list，x 为待查找的数，lo 和 hi 为 a 的上下界，拼合起来意思为：在数组a[lo, hi]中查找x，注意此处同python3列表是左闭右开

参考

• 我作了首诗，保你闭着眼睛也能写对二分查找